Модуль - бәрі естіген сияқты, бірақ іс жүзінде ешкім түсінбейтін нәрселердің бірі. Бүгін солай болады үлкен сабақмодульдері бар теңдеулерді шешуге арналған.

Мен сізге бірден айтамын: сабақ қарапайым болады. Жалпы, модульдер әдетте салыстырмалы түрде қарапайым тақырып болып табылады. «Иә, әрине, оңай! Бұл менің миымды жарып жібереді!» – дейді көптеген студенттер, бірақ бұл мидың бұзылуларының бәрі көпшілігінің басында білім емес, қандай да бір ақымақтық болғандықтан. Ал бұл сабақтың мақсаты – ақылсыздықты білімге айналдыру. :)

Біраз теория

Ендеше кеттік. Ең маңыздысынан бастайық: модуль дегеніміз не? Еске сала кетейін, санның модулі жай ғана бірдей сан, бірақ минус белгісінсіз алынған. Яғни, мысалы, $\left| -5 \right|=5$. Немесе $\left| -129,5\оң|=129,5$.

Бұл қарапайым ма? Иә, қарапайым. Сонда модуль қандай? оң сан? Мұнда бәрі қарапайым: оң санның модулі осы санның өзіне тең: $\left| 5\right|=5$; $\left| 129,5 \right|=129,5$ т.б.

Бір қызық нәрсе шығады: әртүрлі сандарбірдей модуль болуы мүмкін. Мысалы: $\left| -5 \right|=\left| 5\right|=5$; $\left| -129,5 \right|=\left| 129,5 \right|=129,5$. Бұл қандай сандар екенін, модульдері бірдей екенін түсіну оңай: бұл сандар қарама-қарсы. Осылайша, біз модульдерді өзіміз үшін атап өтеміз қарама-қарсы сандартең:

\[\сол| -a \right|=\left| a\right|\]

Тағы бір маңызды факт: модулі ешқашан теріс болмайды. Қандай санды алсақ та - тіпті оң, тіпті теріс - оның модулі әрқашан оң болып шығады (немесе төтенше жағдайларда нөл). Сондықтан модуль жиі санның абсолютті мәні деп аталады.

Сонымен қатар, егер оң және үшін модуль анықтамасын біріктірсек теріс сан, онда біз барлық сандар үшін модульдің ғаламдық анықтамасын аламыз. Атап айтқанда: санның модулі осы санның өзіне тең, егер сан оң болса (немесе нөл), немесе теріс болса, қарама-қарсы санға тең. Сіз мұны формула ретінде жаза аласыз:

Сондай-ақ нөлдік модуль бар, бірақ ол әрқашан нөлге тең. Сонымен қатар, нөл жалғыз сан, оның қарама-қарсылығы жоқ.

Осылайша, $y=\left| функциясын қарастырсақ x \right|$ және оның графигін салуға тырыссаңыз, сіз осындай «таза» аласыз:

Модуль графигі және теңдеулерді шешу мысалы

Мына суреттен сіз бірден $\left| -m \right|=\left| m \right|$, ал модуль сызбасы ешқашан х осінен төмен түспейді. Бірақ бұл бәрі емес: қызыл сызық $y=a$ түзуін белгілейді, ол оң $a$ мәнімен бірден екі түбір береді: $((x)_(1))$ және $((x) _(2)) $, бірақ бұл туралы кейінірек сөйлесеміз. :)

Таза алгебралық анықтамадан басқа геометриялық анықтамасы бар. Сан түзуінде екі нүкте бар делік: $((x)_(1))$ және $((x)_(2))$. Бұл жағдайда $\left| өрнегі ((x)_(1))-((x)_(2)) \right|$ – тек көрсетілген нүктелер арасындағы қашықтық. Немесе, қаласаңыз, осы нүктелерді қосатын сегменттің ұзындығы:

Модуль – сандар түзуіндегі нүктелер арасындағы қашықтық

Сондай-ақ бұл анықтамадан модульдің әрқашан теріс емес екендігі шығады. Бірақ жеткілікті анықтамалар мен теориялар - нақты теңдеулерге көшейік. :)

Негізгі формула

Жарайды, біз анықтаманы анықтадық. Бірақ бұл оңай болған жоқ. Осы модульді қамтитын теңдеулерді қалай шешуге болады?

Тыныш, жай ғана тыныш. Ең қарапайым нәрселерден бастайық. Мынадай нәрсені қарастырыңыз:

\[\сол| x\right|=3\]

Сонымен $x$ модулі 3. $x$ неге тең болуы мүмкін? Анықтама бойынша $x = 3 $ бізге өте қолайлы болады. Шынымен:

\[\сол| 3\оң|=3\]

Басқа сандар бар ма? Қақпақ бар екенін меңзеп тұрғандай. Мысалы, $x=-3$ — $\left| -3 \right|=3$, яғни. қажетті теңдік орындалады.

Ендеше, ізденсек, ойлансақ, тағы да сан табатын шығармыз? Міне, үзіліс: көбірек сандарЖоқ. $\left| теңдеуі x \right|=3$ тек екі түбірі бар: $x=3$ және $x=-3$.

Енді тапсырманы сәл күрделендіріп көрейік. $x$ айнымалысының орнына $f\left(x \right)$ функциясы модуль таңбасының астында ілулі тұрсын, ал оң жағында үштік орнына $a$ ерікті санын қоямыз. Теңдеуді аламыз:

\[\сол| f\left(x \right) \right|=a\]

Ал, сіз қалай шешесіз? Еске сала кетейін: $f\left(x \right)$ — ерікті функция, $a$ — кез келген сан. Анау. кез келген! Мысалы:

\[\сол| 2x+1 \оң|=5\]

\[\сол| 10x-5 \right|=-65\]

Екінші теңдеуді қарастырайық. Сіз ол туралы бірден айта аласыз: оның тамыры жоқ. Неліктен? Бұл дұрыс: өйткені ол модульдің теріс санға тең болуын талап етеді, ол ешқашан болмайды, өйткені біз модуль әрқашан оң сан немесе төтенше жағдайда нөл екенін білеміз.

Бірақ бірінші теңдеумен бәрі қызықтырақ. Екі нұсқа бар: не модуль белгісінің астында оң өрнек бар, содан кейін $\left| 2x+1 \right|=2x+1$, немесе бұл өрнек әлі де теріс, бұл жағдайда $\left| 2x+1 \right|=-\left(2x+1 \right)=-2x-1$. Бірінші жағдайда біздің теңдеу келесі түрде қайта жазылады:

\[\сол| 2x+1 \оңға|=5\Оң жақ көрсеткі 2x+1=5\]

Және кенеттен $2x+1$ ішкі модуль өрнегі шынымен оң болып шықты - ол 5 санына тең. Яғни, біз бұл теңдеуді қауіпсіз шеше аламыз - нәтижесінде алынған түбір жауаптың бір бөлігі болады:

Әсіресе сенбейтіндер табылған түбірді бастапқы теңдеуге ауыстыруға тырысып, модуль астында шынымен оң сан болатынына көз жеткізе алады.

Енді теріс субмодуль өрнегі жағдайын қарастырайық:

\[\сол\( \бастау(туралау)& \сол| 2x+1 \оңға|=5 \\& 2x+1 \lt 0 \\\соңы(туралау) \оңға.\Оң жақ көрсеткі -2x-1=5 \Оң жақ көрсеткі 2x+1=-5\]

Ой! Тағы да бәрі түсінікті: біз $2x+1 \lt 0$ деп болжадық, нәтижесінде $2x+1=-5$ өрнек екенін білдік. нөлден аз. Табылған түбір бізге сәйкес келетініне сенімді бола отырып, нәтиже теңдеуін шешеміз:

Барлығы біз тағы екі жауап алдық: $x=2$ және $x=3$. Иә, есептеулер көлемі өте қарапайым $\left| теңдеуіндегіден сәл артық болып шықты. x \right|=3$, бірақ түбегейлі ештеңе өзгерген жоқ. Мүмкін әмбебап алгоритмнің қандай да бір түрі бар шығар?

Иә, мұндай алгоритм бар. Ал енді біз оны талдаймыз.

Модуль белгісінен құтылу

$\left| теңдеуі берілсін f\left(x \right) \right|=a$, және $a\ge 0$ (әйтпесе, біз бұрыннан білетіндей, түбірлер жоқ). Содан кейін модуль белгісінен келесі ережеге сәйкес құтылуға болады:

\[\сол| f\left(x \right) \right|=a\Оң жақ көрсеткі f\сол(x \оң)=\pm a\]

Осылайша, модулі бар теңдеуіміз екіге бөлінеді, бірақ модульсіз. Бұл бүкіл технология! Бір-екі теңдеуді шешуге тырысайық. Енді осыдан бастайық

\[\сол| 5x+4 \оңға|=10\Оң жақ көрсеткі 5x+4=\pm 10\]

Оң жақта плюс бар он болса, ал минус болғанда бөлек қарастырамыз. Бізде бар:

\[\бастау(туралау)& 5x+4=10\Оң жақ көрсеткі 5x=6\Оң жақ көрсеткі x=\frac(6)(5)=1,2; \\& 5x+4=-10\Оң жақ көрсеткі 5x=-14\Оң жақ көрсеткі x=-\frac(14)(5)=-2,8. \\\соңы(туралау)\]

Осымен болды! Бізде екі түбір бар: $x=1,2$ және $x=-2,8$. Бүкіл шешім сөзбе-сөз екі жолды алды.

Жарайды, сұрақ жоқ, сәл маңыздырақ нәрсені қарастырайық:

\[\сол| 7-5x \right|=13\]

Тағы да, модульді плюс пен минуспен ашыңыз:

\[\бастау(туралау)& 7-5x=13\Оң жақ көрсеткі -5x=6\Оң жақ көрсеткі x=-\frac(6)(5)=-1,2; \\& 7-5x=-13\Оң жақ көрсеткі -5x=-20\Оң жақ көрсеткі x=4. \\\соңы(туралау)\]

Тағы да бірнеше жол - және жауап дайын! Мен айтқанымдай, модульдерде күрделі ештеңе жоқ. Сіз тек бірнеше ережелерді есте сақтауыңыз керек. Сондықтан біз ары қарай жүріп, шынымен де қиынырақ тапсырмаларды жалғастырамыз.

Айнымалы оң жақ корпус

Енді мына теңдеуді қарастырайық:

\[\сол| 3x-2 \right|=2x\]

Бұл теңдеу бұрынғыдан түбегейлі ерекшеленеді. Қалай? Ал $2x$ өрнегінің теңдік белгісінің оң жағында болуы - және оның оң немесе теріс екенін алдын ала біле алмаймыз.

Бұл жағдайда қалай болу керек? Біріншіден, біз мұны біржолата түсінуіміз керек егер теңдеудің оң жағы теріс болса, онда теңдеудің түбірі болмайды- модуль теріс санға тең бола алмайтынын біз қазірдің өзінде білеміз.

Екіншіден, егер оң жақ бөлігі әлі де оң болса (немесе нөлге тең), онда сіз дәл бұрынғыдай әрекет ете аласыз: модульді қосу белгісімен бөлек және минус белгісімен бөлек ашыңыз.

Осылайша, $f\left(x \right)$ және $g\left(x \right)$ ерікті функциялары үшін ережені тұжырымдаймыз:

\[\сол| f\left(x \right) \right|=g\left(x \right)\Оң жақ көрсеткі \сол\( \бастау(туралау)& f\left(x \оң)=\pm g\left(x \оң) ), \\& g\left(x \right)\ge 0. \\\соңы(туралау) \оңға.\]

Біздің теңдеуімізге келетін болсақ, біз мынаны аламыз:

\[\сол| 3x-2 \right|=2x\Оң жақ көрсеткі \солға\( \бастау(туралау)& 3x-2=\pm 2x, \\& 2x\ge 0. \\\соңы(туралау) \оңға.\]

Біз $2x\ge 0$ талабын қандай да бір жолмен орындай аламыз. Соңында біз бірінші теңдеуден алынған түбірлерді ақымақтықпен ауыстырып, теңсіздіктің орындалатын-орындалмайтынын тексере аламыз.

Ендеше теңдеудің өзін шешейік:

\[\бастау(туралау)& 3x-2=2\Оң жақ көрсеткі 3x=4\Оң жақ көрсеткі x=\frac(4)(3); \\& 3x-2=-2\Оң жақ көрсеткі 3x=0\Оң жақ көрсеткі x=0. \\\соңы(туралау)\]

Осы екі түбірдің қайсысы $2x\ge 0$ талабын қанағаттандырады? Иә, екеуі де! Демек, жауап екі сан болады: $x=(4)/(3)\;$ және $x=0$. Бұл шешім. :)

Студенттердің бірі жалықтыра бастады деп ойлаймын? Одан да күрделі теңдеуді қарастырайық:

\[\сол| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\]

Бұл жаман болып көрінгенімен, шын мәнінде бұл «модуль функцияға тең» түріндегі бірдей теңдеу:

\[\сол| f\left(x \right) \right|=g\left(x \right)\]

Және ол дәл осылай шешіледі:

\[\сол| ((x)^(3))-3((x)^(2))+x \right|=x-((x)^(3))\Оң жақ көрсеткі \солға\( \бастау(туралау)& ( (x)^(3))-3((x)^(2))+x=\pm \left(x-((x)^(3)) \оң), \\& x-((x) )^(3))\ge 0. \\\соңы(туралау) \оңға.\]

Біз теңсіздікпен кейінірек айналысамыз - бұл тым қатыгез (шын мәнінде қарапайым, бірақ біз оны шешпейміз). Әзірге алынған теңдеулерді қарастырайық. Бірінші жағдайды қарастырайық - бұл модуль плюс белгісімен кеңейтілген кезде:

\[((x)^(3))-3((x)^(2))+x=x-((x)^(3))\]

Міне, сол жақта бәрін жинап, ұқсастарын әкеліп, не болатынын көру оңай емес. Және бұл келесідей болады:

\[\begin(align)& ((x)^(3))-3((x)^(2))+x=x-((x)^(3)); \\& 2((x)^(3))-3((x)^(2))=0; \\\соңы(туралау)\]

$((x)^(2))$ ортақ коэффициентін жақшадан шығарсақ, өте қарапайым теңдеу аламыз:

\[((x)^(2))\left(2x-3 \right)=0\Оң жақ көрсеткі \left[ \begin(align)& ((x)^(2))=0 \\& 2x-3 =0 \\\соңы(туралау) \оңға.\]

\[((x)_(1))=0;\төрт ((x)_(2))=\frac(3)(2)=1,5.\]

Міне, біз қолдандық маңызды мүліктуынды, ол үшін біз бастапқы көпмүшені көбейткіштерге бөлдік: көбейткіштердің кем дегенде біреуі нөлге тең болғанда көбейтінді нөлге тең болады.

Енді сол сияқты біз модульді минус белгісімен кеңейту арқылы алынған екінші теңдеумен айналысамыз:

\[\begin(align)& ((x)^(3))-3((x)^(2))+x=-\left(x-((x)^(3)) \right); \\& ((x)^(3))-3((x)^(2))+x=-x+((x)^(3)); \\& -3((x)^(2))+2x=0; \\& x\left(-3x+2 \right)=0. \\\соңы(туралау)\]

Қайтадан бірдей нәрсе: факторлардың кем дегенде біреуі нөлге тең болғанда өнім нөлге тең болады. Бізде бар:

\[\left[ \begin(туралау)& x=0 \\& -3x+2=0 \\\соңы(туралау) \оңға.\]

Бізде үш түбір бар: $x=0$, $x=1,5$ және $x=(2)/(3)\;$. Бұл жиынтықтан соңғы жауапқа не кіреді? Мұны істеу үшін бізде қосымша теңсіздік шектеуі бар екенін есте сақтаңыз:

Бұл талапты қалай ескеру керек? Тек табылған түбірлерді ауыстырайық және осы $x$ үшін теңсіздік орындалады ма, жоқ па тексерейік. Бізде бар:

\[\бастау(туралау)& x=0\Оң жақ көрсеткі x-((x)^(3))=0-0=0\ge 0; \\& x=1,5\Оң жақ көрсеткі x-((x)^(3))=1,5-((1,5)^(3)) \lt 0; \\& x=\frac(2)(3)\Оң жақ көрсеткі x-((x)^(3))=\frac(2)(3)-\frac(8)(27)=\frac(10) (27)\ge 0; \\\соңы(туралау)\]

Осылайша, $x=1,5$ түбірі бізге сәйкес келмейді. Және тек екі түбір жауап береді:

\[((x)_(1))=0;\quad ((x)_(2))=\frac(2)(3).\]

Көріп отырғаныңыздай, бұл жағдайда да қиын ештеңе болған жоқ - модульдері бар теңдеулер әрқашан алгоритм бойынша шешіледі. Сізге тек көпмүшеліктер мен теңсіздіктерді жақсы түсіну керек. Сондықтан біз күрделірек тапсырмаларға көшеміз - қазірдің өзінде бір емес, екі модуль болады.

Екі модульді теңдеулер

Осы уақытқа дейін біз ең көп зерттедік қарапайым теңдеулер- бір модуль және тағы бір нәрсе болды. Біз бұл «басқа нәрсені» модульден алыс теңсіздіктің басқа бөлігіне жібердік, осылайша бәрі $\left| сияқты теңдеуге келтіріледі. f\left(x \right) \right|=g\left(x \right)$ немесе одан да қарапайым $\left| f\left(x \right) \right|=a$.

Бірақ балабақшааяқталды - маңыздырақ нәрсені қарастыратын кез келді. Мынадай теңдеулерден бастайық:

\[\сол| f\left(x \right) \right|=\left| g\left(x \right) \right|\]

Бұл «модуль модульге тең» түріндегі теңдеу. Негізінен маңызды нүктебасқа терминдер мен факторлардың болмауы: сол жақта бір ғана модуль, оң жақта тағы бір модуль - және басқа ештеңе жоқ.

Мұндай теңдеулерді шешу біз осы уақытқа дейін зерттегеннен гөрі қиынырақ деп ойлауға болады. Бірақ жоқ: бұл теңдеулер одан да оңай шешіледі. Міне формула:

\[\сол| f\left(x \right) \right|=\left| g\left(x \right) \right|\Оң жақ көрсеткі f\сол(x \оң)=\pm g\сол(x \оң)\]

Барлық! Біз жай ғана субмодуль өрнектерін олардың біреуіне плюс немесе минус белгісімен префикс қою арқылы теңестіреміз. Содан кейін біз алынған екі теңдеуді шешеміз - және түбірлер дайын! Қосымша шектеулер, теңсіздіктер және т.б. Барлығы өте қарапайым.

Бұл мәселені шешуге тырысайық:

\[\сол| 2x+3 \right|=\left| 2x-7 \оңға|\]

Бастауыш сынып Уотсон! Модульдерді ашу:

\[\сол| 2x+3 \right|=\left| 2x-7 \оңға|\Оң жақ көрсеткі 2x+3=\pm \сол(2x-7 \оң)\]

Әрбір жағдайды жеке қарастырайық:

\[\бастау(туралау)& 2x+3=2x-7\Оң жақ көрсеткі 3=-7\Оң жақ көрсеткі \emptyset ; \\& 2x+3=-\сол(2x-7 \оң)\Оң жақ көрсеткі 2x+3=-2x+7. \\\соңы(туралау)\]

Бірінші теңдеудің түбірі жоқ. Өйткені $3=-7$ қашан болады? $x$ қандай мәндері үшін? «$x$ деген не? Сіз таспен ұрылғансыз ба? Мүлдем $x$ жоқ», - дейсіз. Және сіз дұрыс боласыз. Біз $x$ айнымалысына тәуелді емес теңдік алдық және сонымен бірге теңдіктің өзі дұрыс емес. Сондықтан тамыры жоқ.

Екінші теңдеумен бәрі қызықтырақ, бірақ сонымен бірге өте қарапайым:

Көріп отырғаныңыздай, бәрі бір-екі жолда шешілді - біз сызықтық теңдеуден басқа ештеңе күткен жоқпыз. :)

Нәтижесінде соңғы жауап: $x=1$.

Қалай? Қиын ба? Әрине жоқ. Тағы бірдеңе жасап көрейік:

\[\сол| x-1 \right|=\left| ((x)^(2))-3x+2 \оң|\]

Тағы да бізде $\left| сияқты теңдеу бар f\left(x \right) \right|=\left| g\left(x \right) \right|$. Сондықтан біз модуль белгісін ашып, оны бірден қайта жазамыз:

\[((x)^(2))-3x+2=\pm \left(x-1 \оң)\]

Енді біреу сұрайтын шығар: «Ей, бұл не деген ақымақтық? Неліктен плюс-минус сол жағында емес, оң жағында? Сабыр ет, мен бәрін түсіндіремін. Шынында да, біз теңдеуімізді қайта жазуымыз керек еді келесідей:

Содан кейін жақшаларды ашып, барлық мүшелерді теңдік белгісінен бір бағытта жылжыту керек (өйткені теңдеу екі жағдайда да шаршы болатыны анық), содан кейін түбірлерді табу керек. Бірақ сіз мойындауыңыз керек: «плюс-минус» үш мүшенің алдында болғанда (әсіресе осы терминдердің бірі квадрат өрнек болса), бұл «плюс-минус» тек екінің алдында тұрған жағдайға қарағанда күрделірек көрінеді. шарттар.

Бірақ бастапқы теңдеуді келесідей қайта жазуға ештеңе кедергі келтірмейді:

\[\сол| x-1 \right|=\left| ((x)^(2))-3x+2 \оңға|\Оң жақ көрсеткі \солға| ((x)^(2))-3x+2 \right|=\left| x-1 \right|\]

Не болды? Иә, ерекше ештеңе жоқ: жай ғана сол және оң жақтарын ауыстырды. Ақыр соңында өмірімізді біршама жеңілдететін ұсақ-түйек. :)

Жалпы, біз плюс және минус опцияларын қарастыра отырып, бұл теңдеуді шешеміз:

\[\бастау(туралау)& ((x)^(2))-3x+2=x-1\Оң жақ көрсеткі ((x)^(2))-4x+3=0; \\& ((x)^(2))-3x+2=-\сол(x-1 \оң)\Оң жақ көрсеткі ((x)^(2))-2x+1=0. \\\соңы(туралау)\]

Бірінші теңдеудің түбірлері $x=3$ және $x=1$. Екіншісі әдетте дәл квадрат:

\[((x)^(2))-2x+1=((\сол(x-1 \оң))^(2))\]

Сондықтан оның бір түбірі бар: $x=1$. Бірақ біз бұл түбірді ертерек алғанбыз. Осылайша, соңғы жауапқа тек екі сан кіреді:

\[((x)_(1))=3;\төрт ((x)_(2))=1.\]

Тапсырма орындалды! Оны сөреден алып, бәліш жеуге болады. Олардың 2-уі бар, орташа. :)

Маңызды ескерту. Тамырлары бірдей әртүрлі опциялармодульді кеңейту бастапқы көпмүшелердің факторларға ыдырауын білдіреді және бұл факторлардың арасында міндетті түрде ортақ болады. Шынымен:

\[\бастау(туралау)& \left| x-1 \right|=\left| ((x)^(2))-3x+2 \right|; \\&\сол| x-1 \right|=\left| \left(x-1 \right)\left(x-2 \right) \right|. \\\соңы(туралау)\]

Модуль қасиеттерінің бірі: $\left| a\cdot b \right|=\left| a \right|\cdot \left| b \right|$ (яғни, көбейтіндінің модулі модульдер көбейтіндісіне тең), сондықтан бастапқы теңдеуді келесі түрде қайта жазуға болады.

\[\сол| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \оң|\]

Көріп отырғаныңыздай, бізде шынымен ортақ фактор бар. Енді, егер сіз барлық модульдерді бір жағында жинасаңыз, онда бұл көбейткішті жақшадан шығаруға болады:

\[\бастау(туралау)& \left| x-1 \right|=\left| x-1 \right|\cdot \left| x-2 \right|; \\&\сол| x-1 \right|-\left| x-1 \right|\cdot \left| x-2 \right|=0; \\&\сол| x-1 \right|\cdot \left(1-\left| x-2 \right| \right)=0. \\\соңы(туралау)\]

Ал, енді факторлардың кем дегенде біреуі нөлге тең болғанда өнім нөлге тең болатынын еске түсіреміз:

\[\left[ \begin(туралау)& \left| x-1 \right|=0, \\& \left| x-2 \right|=1. \\\соңы(туралау) \оңға.\]

Осылайша, екі модулі бар бастапқы теңдеу біз сабақтың басында айтқан ең қарапайым екі теңдеуге дейін қысқартылды. Мұндай теңдеулерді бірнеше жолда шешуге болады. :)

Бұл ескерту қажетсіз күрделі және іс жүзінде қолданылмайтын болып көрінуі мүмкін. Дегенмен, шын мәнінде, сіз одан да көп нәрсеге тап болуыңыз мүмкін қиын тапсырмаларбіз бүгін талқылайтындарға қарағанда. Оларда модульдер көпмүшелермен, арифметикалық түбірлермен, логарифмдермен және т.б. Мұндай жағдайларда жақшадан бірдеңені шығару арқылы теңдеудің жалпы дәрежесін төмендету мүмкіндігі өте ыңғайлы болуы мүмкін. :)

Енді мен бір қарағанда ақылсыз болып көрінетін тағы бір теңдеуді талдағым келеді. Көптеген студенттер оған «жабысып» қалады, тіпті модульдерді жақсы түсінетініне сенетіндер де.

Дегенмен, бұл теңдеуді шешу біз бұрын қарастырғанға қарағанда оңайырақ. Ал неге екенін түсінсеңіз, модульдері бар теңдеулерді жылдам шешуге арналған тағы бір трюк аласыз.

Сонымен теңдеу:

\[\сол| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \оң|=0\]

Жоқ, бұл қате емес: бұл модульдер арасындағы плюс. Қай $x$ үшін екі модульдің қосындысы нөлге тең екенін табуымыз керек. :)

Қандай проблема? Мәселе мынада, әрбір модуль оң сан немесе төтенше жағдайда нөл. Екі оң санды қосқанда не болады? Әлбетте, қайтадан оң сан:

\[\бастау(туралау)& 5+7=12 \gt 0; \\& 0,004+0,0001=0,0041 \gt 0; \\& 5+0=5 \gt 0. \\\соңы(туралау)\]

Соңғы жол сізге идея бере алады: модульдердің қосындысы нөлге тең болатын жалғыз жағдай, егер әрбір модуль нөлге тең болса:

\[\сол| x-((x)^(3)) \right|+\left| ((x)^(2))+x-2 \оңға|=0\Оң жақ көрсеткі \солға\( \бастау(туралау)& \сол| x-((x)^(3)) \оңға|=0, \\& \left|((x)^(2))+x-2 \right|=0. \\\соңы(туралау) \оңға.\]

Модуль қашан нөлге тең болады? Тек бір жағдайда – ішкі модуль өрнегі нөлге тең болғанда:

\[((x)^(2))+x-2=0\Оң жақ көрсеткі \сол(x+2 \оң)\сол(x-1 \оң)=0\Оң жақ көрсеткі \сол[ \бастау(туралау)& x=-2 \\& x=1 \\\соңы(туралау) \оңға.\]

Осылайша, бізде бірінші модуль нөлге орнатылатын үш нүкте бар: 0, 1 және −1; сондай-ақ екінші модуль нөлге теңестірілген екі нүкте: −2 және 1. Дегенмен, бізге екі модульді бір уақытта нөлге келтіру керек, сондықтан табылған сандардың ішінен екі жиынтыққа кіретіндерді таңдау керек. Әлбетте, мұндай бір ғана сан бар: $x=1$ - бұл соңғы жауап болады.

бөлу әдісі

Міне, біз көптеген тапсырмаларды орындап, көптеген амалдарды үйрендік. Сіз осылай деп ойлайсыз ба? Бірақ жоқ! Енді біз соңғы техниканы қарастырамыз - және сонымен бірге ең маңыздысы. Біз модулі бар теңдеулерді бөлу туралы айтатын боламыз. Не талқыланады? Кішкене артқа шегініп, қарапайым теңдеуді қарастырайық. Мысалы, бұл:

\[\сол| 3x-5\оң|=5-3x\]

Негізінде, біз мұндай теңдеуді қалай шешу керектігін білеміз, өйткені ол солай стандартты дизайн$\left| f\left(x \right) \right|=g\left(x \right)$. Бірақ бұл теңдеуді сәл басқа бұрыштан қарауға тырысайық. Дәлірек айтқанда, модуль белгісінің астындағы өрнекті қарастырыңыз. Естеріңізге сала кетейін, кез келген санның модулі санның өзіне тең болуы мүмкін немесе ол осы санға қарама-қарсы болуы мүмкін:

\[\сол| a \right|=\left\( \бастау(туралау)& a,\quad a\ge 0, \\& -a,\quad a \lt 0. \\\соңы(туралау) \оңға.\]

Шын мәнінде, бұл екіұштылық бүкіл мәселе: модуль астындағы сан өзгеретіндіктен (бұл айнымалыға байланысты), оның оң немесе теріс екендігі бізге түсініксіз.

Бірақ егер біз бастапқыда бұл санның оң болуын талап етсек ше? Мысалы, $3x-5 \gt 0$ деп талап етейік - бұл жағдайда модуль белгісінің астында оң санды алуға кепілдік беріледі және біз бұл модульден толығымен құтыла аламыз:

Осылайша, біздің теңдеу оңай шешілетін сызықтық теңдеуге айналады:

Рас, бұл ойлардың барлығы $3x-5 \gt 0$ жағдайында ғана мағынасы бар - модульді бір мағыналы ашу үшін біз бұл талапты өзіміз енгіздік. Ендеше табылған $x=\frac(5)(3)$ мәнін осы шартқа қойып, тексерейік:

Қашан екені белгілі болды көрсетілген мән$x$ біздің талабымыз қанағаттандырылмайды, өйткені өрнек нөлге тең болды және бізге ол нөлден қатаң түрде үлкен болуы керек. Өкінішті. :(

Бірақ бұл жақсы! Өйткені, $3x-5 \lt 0$ деген тағы бір нұсқа бар. Оның үстіне: $3x-5=0$ жағдайы да бар - мұны да ескеру керек, әйтпесе шешім толық емес болады. Сонымен, $3x-5 \lt 0$ жағдайын қарастырыңыз:

Модуль минус белгісімен ашылатыны анық. Бірақ содан кейін біртүрлі жағдай туындайды: бірдей өрнек бастапқы теңдеудің сол жағында да, оң жағында да көрінеді:

Қызық, қандай $x$ үшін $5-3x$ өрнегі $5-3x$ өрнегіне тең болады? Мұндай теңдеулерден тіпті капитанның да сілекейі тұншығып қалатыны анық, бірақ біз бұл теңдеудің сәйкестік екенін білеміз, яғни. бұл айнымалының кез келген мәні үшін дұрыс!

Бұл кез келген $x $ бізге сәйкес келетінін білдіреді. Дегенмен, бізде шектеу бар:

Басқаша айтқанда, жауап бір сан емес, тұтас интервал болады:

Ақырында, қарастыратын тағы бір жағдай қалды: $3x-5=0$. Мұнда бәрі қарапайым: модуль астында нөл болады, ал нөлдің модулі де нөлге тең (бұл анықтамадан тікелей туындайды):

Бірақ содан кейін бастапқы теңдеу $\left| 3x-5 \right|=5-3x$ келесідей қайта жазылады:

Біз $3x-5 \gt 0$ жағдайын қарастырған кезде бұл түбірді жоғарыда алдық. Сонымен қатар, бұл түбір $3x-5=0$ теңдеуінің шешімі болып табылады - бұл модульді жою үшін біз өзіміз енгізген шектеу. :)

Осылайша, интервалдан басқа, біз осы интервалдың ең соңында жатқан санмен де қанағаттанамыз:

Модульмен теңдеулердегі түбірлерді біріктіру

Жалпы қорытынды жауап: $x\in \left(-\infty ;\frac(5)(3) \right]$. Модульі бар өте қарапайым (негізінен сызықтық) теңдеудің жауабында мұндай келеңсіздікті көру өте жиі кездеседі. Ал, үйреніңіз: модульдің күрделілігі мынада: мұндай теңдеулердің жауаптары мүлдем болжау мүмкін емес.

Тағы бір маңыздысы: біз модулі бар теңдеуді шешудің әмбебап алгоритмін жаңа ғана бөлшектедік! Және бұл алгоритм келесі қадамдардан тұрады:

1. Теңдеудегі әрбір модульді нөлге теңестіріңіз. Кейбір теңдеулерді алайық;
2. Осы теңдеулердің барлығын шешіп, сан түзуіндегі түбірлерді белгіле. Нәтижесінде түзу сызық бірнеше аралықтарға бөлінеді, олардың әрқайсысында барлық модульдер бірегей түрде кеңейтіледі;
3. Әрбір аралық үшін бастапқы теңдеуді шешіңіз және жауаптарды біріктіріңіз.

Осымен болды! Бір ғана сұрақ қалады: 1-қадамда алынған тамырлармен не істеу керек? Бізде екі түбір бар делік: $x=1$ және $x=5$. Олар сандар жолын 3 бөлікке бөледі:

Нүктелер арқылы сан түзуін аралықтарға бөлу

Сонымен, интервалдар қандай? Олардың үшеуі бар екені анық:

1. Ең сол жақта: $x \lt 1$ - бірлік өзі интервалға кірмейді;
2. Орталық: $1\le x \lt 5$ - мұнда біреуі интервалға кіреді, бірақ бесеуі қосылмайды;
3. Ең оң жақ: $x\ge 5$ — бесеуі тек осында қамтылған!

Сіз үлгіні түсіндіңіз деп ойлаймын. Әрбір интервал сол жақ ұшын қамтиды және оң жақ ұшын қамтымайды.

Бір қарағанда, мұндай жазба ыңғайсыз, қисынсыз және жалпы алғанда қандай да бір ақылсыз болып көрінуі мүмкін. Бірақ маған сеніңіз: кішкене тәжірибеден кейін сіз бұл ең сенімді тәсіл екенін және сонымен бірге біржақты ашылатын модульдерге кедергі келтірмейтінін көресіз. Әр жолы ойлағаннан гөрі мұндай схеманы қолданған дұрыс: сол / оң жақ ұшын ағымдағы интервалға беріңіз немесе оны келесіге «лақтырыңыз».

Нұсқау

Егер модуль үздіксіз функция ретінде ұсынылса, онда оның аргументінің мәні оң немесе теріс болуы мүмкін: |х| = x, x ≥ 0; |x| = - x, x

z1 + z2 = (x1 + x2) + i(y1 + y2);
z1 - z2 = (x1 - x2) + i(y1 - y2);

Күрделі сандарды қосу және алу қосу және алу сияқты бірдей ережеге бағынатынын байқау қиын емес.

Екі күрделі санның көбейтіндісі:

z1*z2 = (x1 + iy1)*(x2 + iy2) = x1*x2 + i*y1*x2 + i*x1*y2 + (i^2)*y1*y2.

i^2 = -1 болғандықтан, соңғы нәтиже:

(x1*x2 - y1*y2) + i(x1*y2 + x2*y1).

Күрделі сандар үшін дәрежеге көтеру және түбірін алу операциялары нақты сандармен бірдей анықталады. Алайда, күрделі облыста кез келген сан үшін b^n = a болатындай n саны b, яғни n-ші дәрежелі n түбір бар.

Атап айтқанда, бұл бір айнымалыдағы кез келген n-ші дәрежелі алгебралық теңдеудің дәл n күрделі түбірі бар екенін білдіреді, олардың кейбіреулері және болуы мүмкін.

Қатысты бейнелер

Дереккөздер:

• Дәріс» Күрделі сандар«2019 жылы

Түбір - мұндай санды табудың математикалық операциясын білдіретін белгіше, оны түбір белгісінің алдында көрсетілген дәрежеге көтеру дәл осы белгінің астында көрсетілген санды беруі керек. Көбінесе түбірлері бар мәселелерді шешу үшін тек мәнді есептеу жеткіліксіз. жүзеге асыру керек және қосымша операциялар, олардың бірі түбір белгісінің астындағы санды, айнымалыны немесе өрнекті енгізу.

Нұсқау

Түбірдің көрсеткішін анықтаңыз. Көрсеткіш түбір өрнекті (осы түбір алынған сан) алу үшін түбірді есептеу нәтижесі қандай дәрежеге көтерілу керек екенін көрсететін бүтін сан. Түбір белгішесінің алдында үстіңгі таңба ретінде көрсетілген түбірдің көрсеткіші. Егер бұл анықталмаса, бұл қуаты екі болатын квадрат түбір. Мысалы, √3 түбір көрсеткіші екі, ³√3 көрсеткіші үш, ⁴√3 түбір көрсеткіші төрт және т.б.

Түбір белгісінің астына қосқыңыз келетін санды алдыңғы қадамда анықтаған осы түбірдің көрсеткішіне тең дәрежеге көтеріңіз. Мысалы, ⁴√3 түбір белгісінің астына 5 санын енгізу керек болса, онда түбірдің көрсеткіші төртке тең және 5-ті төртінші дәрежеге көтерудің нәтижесі 5⁴=625 керек. Сіз мұны өзіңізге ыңғайлы кез келген әдіспен жасай аласыз - сіздің ойыңызша, калькуляторды немесе орналастырылған сәйкес қызметтерді пайдалана отырып.

Түбір белгісінің астына алдыңғы қадамда алынған мәнді радикалды өрнектің көбейткіші ретінде енгізіңіз. Алдыңғы қадамда ⁴√3 5 (5*⁴√3) түбірінің астына қосу арқылы қолданылған мысал үшін бұл әрекетті келесідей орындауға болады: 5*⁴√3=⁴√(625*3).

Мүмкін болса, алынған радикалды өрнекті жеңілдетіңіз. Алдыңғы қадамдардағы мысал үшін бұл тек түбір белгісінің астындағы сандарды көбейту керек: 5*⁴√3=⁴√(625*3)=⁴√1875. Бұл түбір астындағы санды қосу әрекетін аяқтайды.

Тапсырмада белгісіз айнымалылар болса, жоғарыда сипатталған қадамдарды ішінде орындауға болады жалпы көрініс. Мысалы, төртінші дәрежелі түбірдің астына белгісіз x айнымалысын енгізгіңіз келсе және түбір өрнегі 5/x³ болса, онда барлық әрекеттер тізбегін келесідей жазуға болады: x*⁴√(5/x³)=⁴ √(x⁴*5/x³)= ⁴√(x*5).

Дереккөздер:

• түбір белгісі қалай аталады

Кез келген мәселені шешу үшін нақты сандар жеткіліксіз квадрат теңдеу. Нақты сандар арасында түбірі жоқ квадрат теңдеулердің ең қарапайымы х^2+1=0. Оны шешкенде x=±sqrt(-1), ал элементар алгебраның заңдары бойынша теріс саннан жұп дәреженің түбірін шығаратыны шығады. сандартыйым салынған.

Студенттер үшін ең қиын тақырыптардың бірі модуль таңбасының астында айнымалысы бар теңдеулерді шешу болып табылады. Алдымен көрейік, бұл немен байланысты? Неліктен, мысалы, квадрат теңдеулерді балалардың көпшілігі жаңғақ сияқты шертеді, бірақ модуль сияқты ең күрделі тұжырымдамадан соншалықты көп проблемалар бар?

Менің ойымша, бұл қиындықтардың барлығы модулі бар теңдеулерді шешудің нақты тұжырымдалған ережелерінің болмауымен байланысты. Сонымен, квадрат теңдеуді шешкен кезде студент алдымен дискриминант формуласын, содан кейін квадрат теңдеудің түбірлерінің формулаларын қолдану керектігін нақты біледі. Бірақ теңдеуде модуль кездессе ше? Біз нақты сипаттауға тырысамыз қажетті жоспартеңдеу модуль таңбасының астында белгісізді қамтитын жағдайға арналған әрекеттер. Біз әр жағдайға бірнеше мысал келтіреміз.

Бірақ алдымен еске түсірейік модуль анықтамасы. Сонымен, санның модулі асанның өзі if деп аталады атеріс емес және -асаны болса анөлден аз. Сіз оны келесідей жаза аласыз:

|а| = a, егер a ≥ 0 және |a| = -a егер а< 0

Модульдің геометриялық мағынасы туралы айтатын болсақ, әрбір нақты сан сан осіндегі белгілі бір нүктеге сәйкес келетінін есте ұстаған жөн. координат. Сонымен, модуль немесе санның абсолюттік мәні осы нүктеден сандық осьтің басына дейінгі қашықтық болып табылады. Қашықтық әрқашан оң сан ретінде беріледі. Сонымен, кез келген теріс санның модулі оң сан болады. Айтпақшы, осы кезеңде де көптеген студенттер шатастыра бастайды. Модульде кез келген сан болуы мүмкін, бірақ модульді қолдану нәтижесі әрқашан оң сан болады.

Енді теңдеулерді шешуге көшейік.

1. |x| түріндегі теңдеуді қарастырайық = c, мұндағы c - нақты сан. Бұл теңдеуді модуль анықтамасы арқылы шешуге болады.

Барлық нақты сандарды үш топқа бөлеміз: нөлден үлкендер, нөлден кішілер және үшінші топ 0 саны. Шешуін сызба түрінде жазамыз:

(±c, c > 0 болса

Егер |x| = c, онда x = (0, егер c = 0 болса

(бар болса, тамыры жоқ< 0

1) |x| = 5, өйткені 5 > 0, содан кейін x = ±5;

2) |x| = -5, өйткені -5< 0, то уравнение не имеет корней;

3) |x| = 0, содан кейін x = 0.

2. |f(x)| түріндегі теңдеу = b, мұндағы b > 0. Шешу үшін берілген теңдеумодульден құтылу керек. Біз мұны былай жасаймыз: f(x) = b немесе f(x) = -b. Енді алынған теңдеулердің әрқайсысын жеке шешу керек. Егер бастапқы теңдеуде b< 0, решений не будет.

1) |x + 2| = 4, өйткені 4 > 0, содан кейін

x + 2 = 4 немесе x + 2 = -4

2) |x 2 – 5| = 11, өйткені 11 > 0, содан кейін

x 2 - 5 = 11 немесе x 2 - 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 түбірлері жоқ

3) |x 2 – 5x| = -8, өйткені -8< 0, то уравнение не имеет корней.

3. |f(x)| түріндегі теңдеу = g(x). Модульдің мағынасына сәйкес, мұндай теңдеудің оң жағы нөлден үлкен немесе тең болса, оның шешімдері болады, яғни. g(x) ≥ 0. Сонда бізде:

f(x) = g(x)немесе f(x) = -g(x).

1) |2x – 1| = 5x - 10. Бұл теңдеудің түбірлері болады, егер 5x - 10 ≥ 0. Мұндай теңдеулерді шешу осы жерден басталады.

1. О.Д.З. 5x – 10 ≥ 0

2. Шешуі:

2x - 1 = 5x - 10 немесе 2x - 1 = -(5x - 10)

3. O.D.Z біріктіріңіз. және шешім, біз аламыз:

Түбір x \u003d 11/7 O.D.Z. сәйкес келмейді, ол 2-ден аз, ал x \u003d 3 бұл шартты қанағаттандырады.

Жауабы: x = 3

2) |x – 1| \u003d 1 - x 2.

1. О.Д.З. 1 - x 2 ≥ 0. Бұл теңсіздікті интервал әдісі арқылы шешейік:

(1 – x)(1 + x) ≥ 0

2. Шешуі:

x - 1 \u003d 1 - x 2 немесе x - 1 \u003d - (1 - x 2)

x 2 + x - 2 = 0 x 2 - x = 0

x = -2 немесе x = 1 x = 0 немесе x = 1

3. Ерітінді мен O.D.Z. біріктіріңіз:

Тек x = 1 және x = 0 түбірлері қолайлы.

Жауабы: x = 0, x = 1.

4. |f(x)| түріндегі теңдеу = |g(x)|. Мұндай теңдеу f(x) = g(x) немесе f(x) = -g(x) келесі екі теңдеумен тең.

1) |x 2 - 5x + 7| = |2x – 5|. Бұл теңдеу келесі екіге тең:

x 2 - 5x + 7 = 2x - 5 немесе x 2 - 5x +7 = -2x + 5

x 2 - 7x + 12 = 0 x 2 - 3x + 2 = 0

x = 3 немесе x = 4 x = 2 немесе x = 1

Жауабы: x = 1, x = 2, x = 3, x = 4.

5. Ауыстыру әдісімен шешілетін теңдеулер (айнымалының өзгеруі). Бұл әдісшешімдерді түсіндіру оңай нақты мысал. Сонымен, модулі бар квадрат теңдеу берілсін:

x 2 – 6|x| + 5 = 0. Модуль қасиеті бойынша x 2 = |x| 2, сондықтан теңдеуді келесі түрде қайта жазуға болады:

|x| 2–6|x| + 5 = 0. |x| өзгертуін жасайық = t ≥ 0 болса, бізде:

t 2 - 6t + 5 \u003d 0. Бұл теңдеуді шеше отырып, t \u003d 1 немесе t \u003d 5 екенін аламыз. Ауыстыруға оралайық:

|x| = 1 немесе |x| = 5

x = ±1 x = ±5

Жауабы: x = -5, x = -1, x = 1, x = 5.

Басқа мысалды қарастырайық:

x 2 + |x| – 2 = 0. Модуль қасиеті бойынша x 2 = |x| 2, сондықтан

|x| 2 + |x| – 2 = 0. |x| өзгертуін енгізейік = t ≥ 0, онда:

t 2 + t - 2 \u003d 0. Осы теңдеуді шешіп, аламыз, t \u003d -2 немесе t \u003d 1. Ауыстыруға оралайық:

|x| = -2 немесе |x| = 1

Түбірлері жоқ x = ± 1

Жауабы: x = -1, x = 1.

6. Теңдеулердің тағы бір түрі «күрделі» модулі бар теңдеулер. Мұндай теңдеулерге «модуль ішіндегі модульдері» бар теңдеулер жатады. Бұл түрдегі теңдеулерді модульдің қасиеттері арқылы шешуге болады.

1) |3 – |x|| = 4. Біз екінші типті теңдеулердегідей әрекет етеміз. Өйткені 4 > 0, онда екі теңдеу аламыз:

3 – |x| = 4 немесе 3 – |x| = -4.

Енді әрбір теңдеудегі х модулін өрнектеп алайық, содан кейін |x| = -1 немесе |x| = 7.

Алынған теңдеулердің әрқайсысын шешеміз. Бірінші теңдеуде түбірлер жоқ, өйткені -1< 0, а во втором x = ±7.

Жауабы x = -7, x = 7.

2) |3 + |x + 1|| = 5. Бұл теңдеуді ұқсас жолмен шешеміз:

3 + |x + 1| = 5 немесе 3 + |x + 1| = -5

|x + 1| = 2 |x + 1| = -8

x + 1 = 2 немесе x + 1 = -2. Тамырлар жоқ.

Жауабы: x = -3, x = 1.

Сондай-ақ бар жалпы әдісмодулі бар теңдеулерді шешу. Бұл интервал әдісі. Бірақ біз оны әрі қарай қарастырамыз.

сайт, материалды толық немесе ішінара көшіру арқылы дереккөзге сілтеме қажет.

Санның абсолютті мәні абасынан нүктеге дейінгі қашықтық А(а).

Бұл анықтаманы түсіну үшін айнымалының орнына ауыстырамыз акез келген сан, мысалы 3 және оны қайта оқып көріңіз:

Санның абсолютті мәні 3 басынан нүктеге дейінгі қашықтық А(3 ).

Модуль әдеттегі қашықтықтан басқа ештеңе емес екені белгілі болды. Бастапқы нүктеден А нүктесіне дейінгі қашықтықты көруге тырысайық( 3 )

Координаталар басынан А нүктесіне дейінгі қашықтық( 3 ) 3-ке тең (үш бірлік немесе үш қадам).

Санның модулі екі тік сызықпен көрсетіледі, мысалы:

3 санының модулі былай белгіленеді: |3|

4 санының модулі былай белгіленеді: |4|

5 санының модулі былай белгіленеді: |5|

Біз 3 санының модулін іздеп, оның 3-ке тең екенін білдік. Сонымен былай жазамыз:

Мынадай оқиды: «Үштің модулі үш»

Енді -3 санының модулін тауып көрейік. Тағы да анықтамаға ораламыз және оның орнына -3 санын қоямыз. Тек нүктенің орнына Апайдалану жаңа нүкте Б. Нүкте Абіз бірінші мысалда қолдандық.

Санның модулі 3 басынан нүктеге дейінгі қашықтықты атайды Б(—3 ).

Бір нүктеден екіншісіне дейінгі қашықтық теріс болуы мүмкін емес. Демек, қашықтық бола отырып, кез келген теріс санның модулі де теріс болмайды. -3 санының модулі 3 саны болады. Бастапқы нүктеден В(-3) нүктесіне дейінгі қашықтық үш бірлікке тең:

Мынадай оқиды: «Санның модулі үш минус үш»

0 санының модулі 0-ге тең, өйткені координатасы 0 болатын нүкте координаталық нүктемен сәйкес келеді, яғни. басынан нүктеге дейінгі қашықтық O(0)нөлге тең:

«Нөлдің модулі нөлге тең»

Біз қорытынды жасаймыз:

• Санның модулі теріс болуы мүмкін емес;
• Оң сан және нөл үшін модуль санның өзіне, ал теріс үшін қарама-қарсы санға тең;
• Қарама-қарсы сандардың модульдері бірдей.

Қарама-қарсы сандар

Таңбалары бойынша ғана ерекшеленетін сандар аталады қарама-қарсы. Мысалы, −2 және 2 сандары қарама-қарсы сандар. Олар тек белгілер бойынша ерекшеленеді. −2 санында минус, ал 2 санында плюс таңбасы бар, бірақ біз оны көрмейміз, өйткені плюс, бұрын айтқанымыздай, дәстүрлі түрде жазылмайды.

Қарама-қарсы сандарға көбірек мысалдар:

Қарама-қарсы сандардың модульдері бірдей. Мысалы, −2 және 2 модульдерін табайық

Суретте басынан нүктелерге дейінгі қашықтық көрсетілген A(−2)Және B(2)екі қадамға тең.

Сізге сабақ ұнады ма?
Біздің қосылыңыз жаңа топВконтакте және жаңа сабақтар туралы хабарландырулар алуды бастаңыз

МБОУ No17 орта мектебі, Иванов

« Модульдік теңдеулер»
Әдістемелік өңдеу

Құрастырылған

математика мұғалімі

Лебедева Н.В.

20010

түсіндірме жазба

1-тарау Кіріспе

2-бөлім. Негізгі мүмкіндіктер Бөлім 3. Санның модулі түсінігінің геометриялық түсіндірмесі 4-бөлім. y = |x| функциясының графигі 5-бөлім Конвенциялар

2-тарау

1-бөлім. |F(х)| түріндегі теңдеулер = м (қарапайымдылар) 2-бөлім. F(|х|) = m түріндегі теңдеулер 3-бөлім. |F(х)| түріндегі теңдеулер = G(x) 4-бөлім. |F(х)| түріндегі теңдеулер = ± F(x) (әдемі) 5-бөлім. |F(х)| түріндегі теңдеулер = |G(x)| Бөлім 6. Стандартты емес теңдеулерді шешу мысалдары 7-бөлім. |F(х)| түріндегі теңдеулер + |G(x)| = 0 8-бөлім. |а 1 x ± в 1 | түріндегі теңдеулер ± |a 2 x ± в 2 | ± …|a n x ± in n | = м 9-бөлім. Құрамында бірнеше модуль бар теңдеулер

3-тарау. Модульі бар әртүрлі теңдеулерді шешу мысалдары.

1-бөлім. Тригонометриялық теңдеулер 2-бөлім көрсеткіштік теңдеулер 3-бөлім Логарифмдік теңдеулер 4-бөлім. Иррационал теңдеулер 5-бөлім. Күрделілігі жоғары тапсырмалар Жаттығулардың жауаптары Әдебиеттер тізімі

Түсіндірме жазба.

Абсолюттік шама (модуль) түсінігі нақты саноның маңызды қасиеттерінің бірі болып табылады. Бұл тұжырымдама бар кең қолдануфизика, математика және техника ғылымдарының әртүрлі бөлімдерінде. жылы математика курсын оқыту тәжірибесінде орта мектепРесей Федерациясы Қорғаныс министрлігінің Бағдарламасына сәйкес «санның абсолютті мәні» түсінігі бірнеше рет кездеседі: 6-сыныпта модульдің анықтамасы, оның геометриялық мағынасы енгізіледі; 8-сыныпта абсолютті қате туралы түсінік қалыптасады, модулі бар қарапайым теңдеулер мен теңсіздіктердің шешімі қарастырылады, арифметиканың қасиеттері. шаршы түбір; 11-сыныпта «Түбір nші дәреже».Оқыту тәжірибесі студенттердің білімді қажет ететін тапсырмаларды шешуде жиі қиындықтарға тап болатынын көрсетеді бұл материал, және орындауды бастамай-ақ жиі өткізіп жібереді. 9-11-сыныптар курсы бойынша емтихан тапсырмаларының мәтіндерінде де осыған ұқсас тапсырмалар берілген. Сонымен қатар, университеттердің мектеп түлектеріне қоятын талаптары әртүрлі, атап айтқанда, көбірек жоғары деңгеймектеп бағдарламасының талаптарына қарағанда. Өмір үшін қазіргі қоғамбелгілі бір психикалық дағдыларда көрінетін ойлаудың математикалық стилін қалыптастыру өте маңызды. Модульдермен есептерді шешу барысында жалпылау және нақтылау, талдау, жіктеу және жүйелеу, аналогия сияқты әдіс-тәсілдерді қолдана білу қажет. Мұндай тапсырмаларды шешу негізгі бөлімдер бойынша білімдерін тексеруге мүмкіндік береді мектеп курсы, логикалық ойлау деңгейі, зерттеу әрекетінің бастапқы дағдылары. бұл жұмысбөлімдердің біріне – модулі бар теңдеулерді шешуге арналған. Ол үш тараудан тұрады. Бірінші тарауда негізгі ұғымдар мен маңызды теориялық есептеулер берілген. Екінші тарауда модулі бар теңдеулердің тоғыз негізгі түрі ұсынылады, оларды шешу әдістері қарастырылады және мысалдар талданады. әртүрлі деңгейлерқиындықтар. Үшінші тарауда анағұрлым күрделі және стандартты емес теңдеулер (тригонометриялық, көрсеткіштік, логарифмдік және иррационалдық) ұсынылған. Әрбір теңдеу түріне арналған жаттығулар бар тәуелсіз шешім(жауаптар мен нұсқаулар қоса беріледі). Бұл жұмыстың негізгі мақсаты мұғалімдерге сабаққа дайындалуда және факультативтік курстарды ұйымдастыруда әдістемелік көмек көрсету болып табылады. материал ретінде де пайдалануға болады оқу құралыжоғары сынып оқушыларына арналған. Жұмыста ұсынылған тапсырмалар қызықты және әрқашан оңай шешілмейді, бұл студенттердің оқу мотивациясын саналы етуге, олардың қабілеттерін тексеруге және мектеп түлектерінің жоғары оқу орындарына түсуге дайындық деңгейін арттыруға мүмкіндік береді. Ұсынылған жаттығуларды сараланған таңдау материалды игерудің репродуктивті деңгейінен шығармашылық деңгейге көшуді, сондай-ақ стандартты емес есептерді шешуде өз білімін қолдануды үйрету мүмкіндігін білдіреді.

1-тарау. Кіріспе.

1-бөлім. Абсолюттік шаманы анықтау .

Анықтама : Нақты санның абсолютті мәні (модуль). Атеріс емес сан деп аталады: Анемесе -А. Белгіленуі: │ А │ Жазба келесідей оқылады: «a санының модулі» немесе «а санының абсолютті мәні»

│ a, егер a > 0

│a│ = │ 0, егер a = 0 (1)

│ - а, егер а
Мысалдар: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Өрнек модулін кеңейту:

а) │x - 8│, егер x > 12 б) │2x + 3│, егер x ≤ -2 │x - 8│= x - 8 │ 2x + 3│= - 2x - 3

2-бөлім. Негізгі қасиеттер.

Абсолюттік шаманың негізгі қасиеттерін қарастырайық. №1 қасиет: Қарама-қарсы сандар бірдей модульдерге ие, яғни. │а│=│-а│Теңдіктің дұрыстығын көрсетейік. Санның анықтамасын жазып алайық - А : │- a│= (2) (1) және (2) жиындарын салыстырайық. Анықтамалар екені анық абсолютті мәндерсандар АЖәне - Асәйкестендіріңіз. Демек, │а│=│-а│
Төмендегі қасиеттерді қарастырған кезде біз олардың тұжырымдарымен шектелеміз, өйткені олардың дәлелі келтірілген №2 қасиет: Нақты сандардың соңғы санының қосындысының абсолютті мәні терминдердің абсолютті мәндерінің қосындысынан аспайды: №3 қасиет: Екі нақты санның айырмашылығының абсолюттік мәні олардың абсолюттік мәндерінің қосындысынан аспайды: │а - в│ ≤│а│+│в│ №4 мүлік: Нақты сандардың ақырлы санының көбейтіндісінің абсолютті мәні мына факторлардың абсолютті мәндерінің көбейтіндісіне тең: │а · в│=│а│·│в│ №5 мүлік: Нақты сандар бөлігінің абсолютті мәні олардың абсолюттік мәндерінің бөліміне тең:

Бөлім 3. Санның модулі түсінігінің геометриялық түсіндірмесі.

Әрбір нақты санды сан түзуіндегі нүктемен байланыстыруға болады, ол осы нақты санның геометриялық көрінісі болады. Сандық түзудегі әрбір нүкте оның басынан қашықтығына сәйкес келеді, яғни. кесіндінің басынан берілген нүктеге дейінгі ұзындығы. Бұл қашықтық әрқашан теріс емес мән ретінде қарастырылады. Демек, сәйкес кесіндінің ұзындығы берілген нақты санның абсолютті мәнінің геометриялық түсіндірмесі болады

Ұсынылған геометриялық иллюстрация №1 сипатты анық растайды, яғни. қарама-қарсы сандардың модульдері тең. Осы жерден теңдіктің дұрыстығын оңай түсінуге болады: │x - a│= │a - x│. Сондай-ақ │х│= m теңдеуін шешу айқынырақ болады, мұндағы m ≥ 0, атап айтқанда x 1,2 = ± m. Мысалдар: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; 4

4-бөлім. y \u003d │х│ функциясының графигі

Бұл функцияның анықталу облысы барлық нақты сандар болып табылады.

5-бөлім. Рәміздер.

Болашақта теңдеулерді шешу мысалдарын қарастыру кезінде келесілер қолданылады. шартты белгілер: ( - жүйе белгісі [ - орнату белгісі Теңдеулер (теңсіздіктер) жүйесін шешу кезінде жүйеге кіретін теңдеулердің (теңсіздіктердің) шешімдерінің қиылысуы табылады. Теңдеулер (теңсіздіктер) жиынын шешу кезінде жиынға кіретін теңдеулердің (теңсіздіктердің) шешімдерінің бірігуі табылады.

2-тарау

Бұл тарауда біз бір немесе бірнеше модульден тұратын теңдеулерді шешудің алгебралық жолдарын қарастырамыз.

1-бөлім. │F (х) │= m түріндегі теңдеулер

Бұл түрдегі теңдеу ең қарапайым деп аталады. Оның шешімі m ≥ 0 болған жағдайда ғана болады. Модульдің анықтамасы бойынша бастапқы теңдеу екі теңдеудің қосындысына тең: │ Ф(x)│=м
Мысалдар:
№1. Теңдеуді шешіңіз: │7x - 2│= 9


Жауабы: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = -1; x 2 \u003d -2 x (x + 3) \u003d 0 x 1 \u003d 0; x 2 = -3 Жауабы: түбірлердің қосындысы – 2.№3
│x 4 -5x 2 + 2│= 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 x 2 = m, m ≥ 0 x = 0 деп белгілейді; ±√5 м 2 – 5м + 4 = 0 м = 1; 4 – екі мән де m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 шартын қанағаттандырады Жауабы: 7-теңдеудің түбірлерінің саны. Жаттығулар:
№1. Теңдеуді шешіп, түбірлердің қосындысын көрсет: │x - 5│= 3 №2 . Теңдеуді шешіп, кіші түбірін көрсетіңіз: │x 2 + x │ \u003d 0 №3 . Теңдеуді шешіп, үлкенірек түбірін көрсетіңіз: │x 2 - 5x + 4 │ \u003d 4 №4 .Теңдеуді шешіп, бүтін түбірді көрсет: │2x 2 - 7x + 6│ \u003d 1 №5 .Теңдеуді шешіп, түбірлер санын көрсет: │x 4 - 13x 2 + 50 │ = 14

2-бөлім. F(│х│) = m түріндегі теңдеулер

Сол жағындағы функция аргументі модуль белгісінің астында, ал оң жағы айнымалыға тәуелсіз. Осы түрдегі теңдеулерді шешудің екі әдісін қарастырайық. 1 жол:Абсолюттік шаманың анықтамасы бойынша бастапқы теңдеу екі жүйенің жиынтығына тең. Олардың әрқайсысында субмодуль өрнекіне шарт қойылады. Ф(│х│) =м
F(│х│) функциясы барлық анықтау облысында жұп болғандықтан, F(х) = m және F(-х) = m теңдеулерінің түбірлері қарама-қарсы сандар жұптары болып табылады. Сондықтан жүйенің біреуін шешу жеткілікті (мысалдарды осылай қарастырғанда бір жүйенің шешімі беріледі). 2 жол:Жаңа айнымалыны енгізу әдісін қолдану. Бұл жағдайда │х│= a белгілеу енгізіледі, мұнда a ≥ 0. Бұл әдіс конструкцияда аз көлемді.
Мысалдар: №1 . Теңдеуді шешіңіз: 3x 2 - 4│x│ = - 1 Жаңа айнымалы енгізуді қолданайық. │х│= a деп белгілеңіз, мұндағы a ≥ 0. 3a 2 - 4a + 1 = 0 теңдеуін аламыз D = 16 - 12 = 4 a 1 = 1 a 2 = 1 / 3 Бастапқы айнымалыға ораламыз: │х │ = 1 және │х│= 1/3. Әрбір теңдеудің екі түбірі болады. Жауабы: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Теңдеуді шешіңіз: 5x 2 + 3│x│- 1 \u003d 1/2 │x│ + 3x 2
Бірінші жиын жүйесінің шешімін табайық: 4x 2 + 5x - 2 \u003d 0 D \u003d 57 x 1 \u003d -5 + √57 / 8 x 2 \u003d -5-√57 / 8 x 2 орындайтынын ескеріңіз. x ≥ 0 шартын қанағаттандырмайды. Шешімі бойынша екінші жүйе қарама-қарсы x 1 саны болады. Жауабы: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Теңдеуді шешіңіз: x 4 - │х│= 0 │х│= a деп белгілеңіз, мұндағы a ≥ 0. a 4 - a \u003d 0 a (a 3 - 1) \u003d 0 a 1 \u003d 0 теңдеуін аламыз. a 2 \u003d 1 Біз бастапқы айнымалыға ораламыз: │х│=0 және │х│= 1 x = 0; ± 1 Жауабы: x 1 = 0; X 2 = 1; X 3 = - 1.
Жаттығулар: №6. Теңдеуді шешіңіз: 2│х│ - 4,5 = 5 - 3/8 │х│ №7 . Теңдеуді шешіңіз, жауапта түбірлер санын көрсетіңіз: 3x 2 - 7│x│ + 2 = 0 №8 . Теңдеуді шешіңіз, жауапта барлық шешімдерді көрсетіңіз: x 4 + │х│ - 2 = 0

3-бөлім. │F(х)│ = G(х) түріндегі теңдеулер

Бұл түрдегі теңдеудің оң жағы айнымалыға тәуелді және сондықтан, егер оң жағы G(x) ≥ 0 функциясы болса ғана шешімі болады. Бастапқы теңдеуді екі жолмен шешуге болады: 1 жол:Стандарт, оның анықтамасына негізделген модульді ашуға негізделген және екі жүйенің тіркесіміне эквивалентті өтуден тұрады. │ Ф(x)│ =Г(X)

Бұл әдісті G(x) функциясы үшін күрделі өрнек және F(x) функциясы үшін күрделі өрнек болған жағдайда қолдану ұтымды, өйткені ол теңсіздіктерді F(x) функциясымен шешу керек. 2 жол:Ол оң жаққа шарт қойылған эквивалентті жүйеге көшуден тұрады. │ Ф(x)│= Г(x)

Бұл әдісті қолдану ыңғайлырақ, егер G(x) функциясының өрнегі F(x) функциясына қарағанда күрделірек болса, өйткені G(x) ≥ 0 теңсіздігінің шешімі қабылданған.Сонымен қатар, жағдайда бірнеше модульдерден, бұл әдіс екінші опцияны пайдалану ұсынылады. Мысалдар: №1. Теңдеуді шешіңіз: │x + 2│= 6 -2x
(1 жол) Жауабы: x = 1 1 / 3 №2.
│x 2 - 2x - 1 │ \u003d 2 (x + 1)
(2 жол) Жауабы: Тамырлардың көбейтіндісі 3-ке тең.
№3. Теңдеуді шеш, жауапта түбірлердің қосындысын жаз:
│x - 6 │ \u003d x 2 - 5x + 9

Жауабы: түбірлердің қосындысы 4-ке тең.
Жаттығулар: №9. │x + 4│= - 3x №10. Теңдеуді шешіңіз, жауапта шешімдер санын көрсетіңіз: │x 2 + x - 1 │ \u003d 2x - 1 №11 . Теңдеуді шешіңіз, жауапта түбірлердің көбейтіндісін көрсетіңіз: │x + 3 │ \u003d x 2 + x - 6

4-бөлім. │F(x)│= F(x) және │F(x)│= - F(x) түріндегі теңдеулер

Бұл түрдегі теңдеулерді кейде «әдемі» деп те атайды. Теңдеулердің оң жағы айнымалыға тәуелді болғандықтан, оң жағы теріс емес болса ғана шешімдер бар. Демек, бастапқы теңдеулер теңсіздіктерге тең:
│F(x)│= F(x) F(x) ≥ 0 және │F(x)│= - F(x) F(x) Мысалдар: №1 . Теңдеуді шешіңіз, жауапта кіші бүтін түбірді көрсетіңіз: │5x - 3│ \u003d 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Жауабы: x = 1№2. Теңдеуді шешіңіз, жауапта аралық ұзындығын көрсетіңіз: │x 2 - 9 │ \u003d 9 - x 2 x 2 - 9 ≤ 0 (x - 3) (x + 3) ≤ 0 [- 3; 3] Жауабы: саңылаудың ұзындығы 6.№3 . Теңдеуді шешіңіз, жауапта бүтін шешімдердің санын көрсетіңіз: │2 + x - x 2 │ = 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1; 2] Жауабы: 4 бүтін шешім.№4 . Теңдеуді шешіңіз, жауапта ең үлкен түбірді көрсетіңіз:
│4 - x -
│= 4 – x –
x 2 - 5x + 5 \u003d 0 D \u003d 5 x 1,2 \u003d
≈ 1,4

Жауабы: x = 3.

Жаттығулар: №12. Теңдеуді шешіңіз, жауапта бүтін түбірді көрсетіңіз: │x 2 + 6x + 8 │= x 2 + 6x + 8 №13. Теңдеуді шешіңіз, жауапта бүтін шешімдердің санын көрсетіңіз: │13x - x 2 - 36│+ x 2 - 13x + 36 = 0 №14. Теңдеуді шешіңіз, жауапта теңдеудің түбірі болып табылмайтын бүтін санды көрсетіңіз:

5-бөлім. │F(x)│= │G(x)│ түріндегі теңдеулер

Теңдеудің екі жағы да теріс емес болғандықтан, шешім екі жағдайды қарастырады: ішкі модуль өрнектері таңбалары бойынша тең немесе қарама-қарсы. Демек, бастапқы теңдеу екі теңдеудің қосындысына тең: │ Ф(x)│= │ Г(x)│
Мысалдар: №1. Теңдеуді шешіңіз, жауапта толық түбірді көрсетіңіз: │x + 3│ \u003d │2x - 1│
Жауабы: бүтін түбір x = 4.№2. Теңдеуді шеш: │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
Жауабы: x = 2.№3 . Теңдеуді шешіңіз, жауапта түбірлердің көбейтіндісін көрсетіңіз:




4x 2 + 2x - 1 \u003d 0 x 1,2 \u003d - 1±√5 / 4 теңдеуінің түбірлері Жауабы: түбірлердің көбейтіндісі 0,25. Жаттығулар: №15 . Теңдеуді шешіңіз, жауапта барлық шешімді көрсетіңіз: │x 2 - 3x + 2│ \u003d │x 2 + 6x - 1│ №16. Теңдеуді шешіңіз, жауапта кіші түбірді көрсетіңіз: │5x - 3│=│7 - x│ №17 . Теңдеуді шеш, жауапта түбірлердің қосындысын жаз:

Бөлім 6. Стандартты емес теңдеулерді шешу мысалдары

Бұл бөлімде стандартты емес теңдеулердің мысалдарын қарастырамыз, оларды шешуде өрнектің абсолютті мәні анықтамасы арқылы ашылады. Мысалдар:

№1. Теңдеуді шешіңіз, жауапта түбірлердің қосындысын көрсетіңіз: x │x│- 5x - 6 \u003d 0
Жауабы: түбірлердің қосындысы 1-ге тең №2. . Теңдеуді шешіңіз, жауапта кіші түбірді көрсетіңіз: x 2 - 4x
- 5 = 0
Жауабы: кіші түбір x = - 5. №3. Теңдеуді шеш:

Жауабы: x = -1. Жаттығулар: №18. Теңдеуді шешіп, түбірлердің қосындысын жаз: x │3x + 5│= 3x 2 + 4x + 3
№19. Теңдеуді шешіңіз: x 2 - 3x \u003d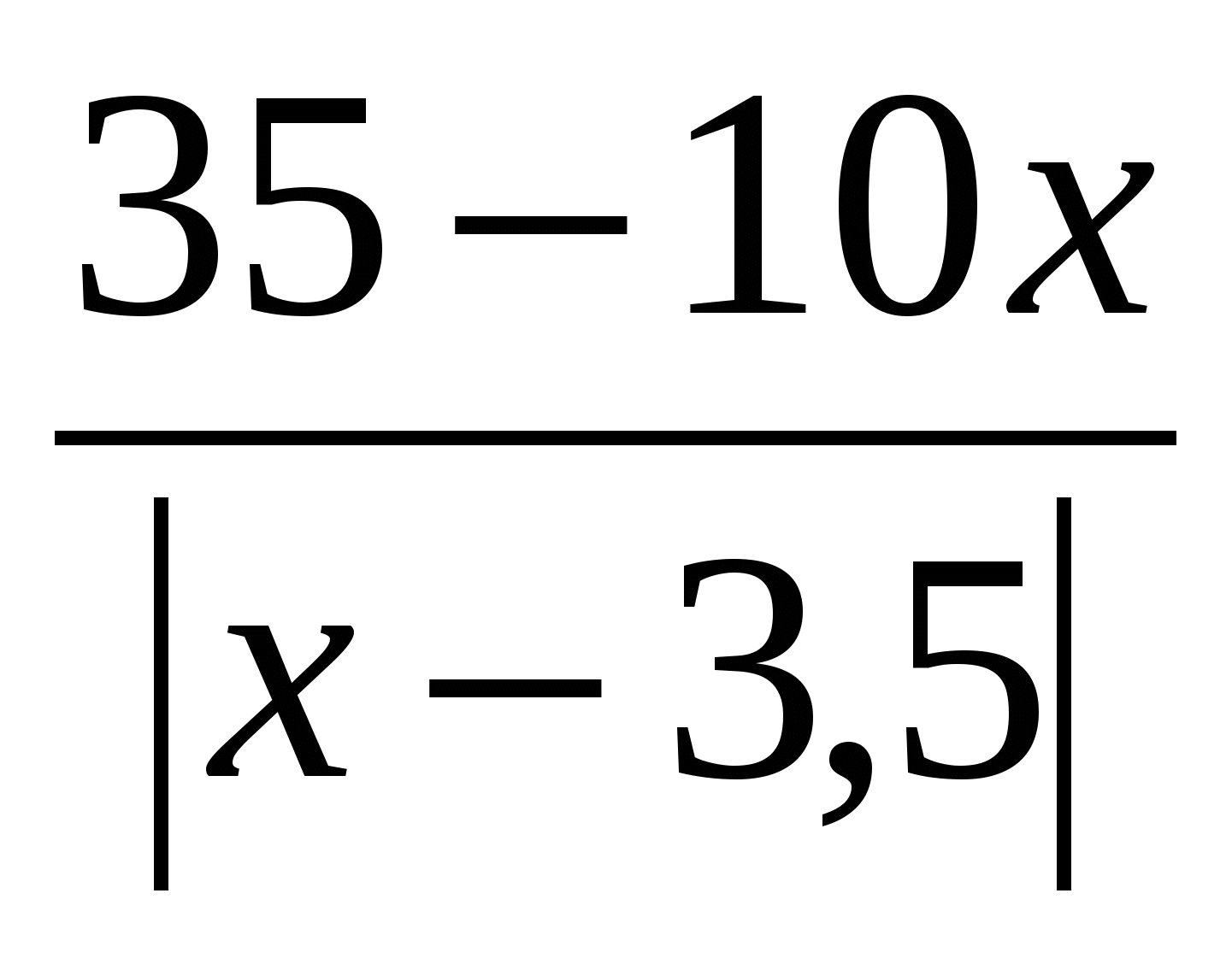

№20. Теңдеуді шеш:

7-бөлім. │F(x)│+│G(x)│=0 түріндегі теңдеулер

Бұл түрдегі теңдеудің сол жағында теріс емес шамалардың қосындысы болатынын байқау қиын емес. Демек, бастапқы теңдеудің шешімі екі мүшесі бір уақытта нөлге тең болған жағдайда ғана болады. Теңдеу теңдеулер жүйесіне эквивалентті: │ Ф(x)│+│ Г(x)│=0
Мысалдар: №1 . Теңдеуді шеш:
Жауабы: x = 2. №2. Теңдеуді шеш: Жауабы: x = 1. Жаттығулар: №21. Теңдеуді шеш: №22 . Теңдеуді шеш, жауапта түбірлердің қосындысын жаз: №23 . Теңдеуді шешіңіз, жауапта шешімдер санын көрсетіңіз:

8-бөлім. Пішіннің теңдеуі

Бұл түрдегі теңдеулерді шешу үшін интервалдар әдісі қолданылады. Егер ол модульдерді дәйекті кеңейту арқылы шешілсе, онда біз аламыз nжүйелер жиынтығы, бұл өте ауыр және қолайсыз. Интервал әдісінің алгоритмін қарастырайық: 1). Айнымалы мәндерді табыңыз X, ол үшін әрбір модуль нөлге тең (ішкі модуль өрнектерінің нөлдері):
2). Табылған мәндер аралықтарға бөлінген сан жолында белгіленеді (тиісінше интервалдар саны тең n+1 ) 3). Әрбір алынған аралықта әрбір модуль қандай белгімен ашылатынын анықтаңыз (шешімді жасаған кезде ондағы белгілерді белгілей отырып, сандық сызықты қолдануға болады) 4). Бастапқы теңдеу жиынға эквивалентті n+1 жүйелер, олардың әрқайсысында айнымалының мүшелігі көрсетілген Xаралықтардың бірі. Мысалдар: №1 . Теңдеуді шешіңіз, жауапта ең үлкен түбірді көрсетіңіз:
1). Ішкі модульдік өрнектердің нөлдерін табайық: x = 2; x = -3 2). Табылған мәндерді сандық сызықта белгілейміз және алынған интервалдарда әрбір модуль қандай белгімен ашылатынын анықтаймыз:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- шешімі жоқ Теңдеудің екі түбірі бар. Жауабы: ең үлкен түбір х = 2. №2. Теңдеуді шешіңіз, жауапта түбірді түгел жазыңыз:
1). Ішкі модуль өрнектерінің нөлдерін табайық: x = 1,5; x = - 1 2). Табылған мәндерді сандық сызықта белгілейміз және алынған интервалдарда әрбір модуль қандай белгімен ашылатынын анықтаймыз: x + 1 x + 1 x + 1 - + +
-1 1,5 х 2х – 3 2х – 3 2х – 3 - - +
3).
Соңғы жүйенің шешімі жоқ, сондықтан теңдеудің екі түбірі бар. Теңдеуді шешкен кезде екінші модульдің алдындағы «-» белгісіне назар аудару керек. Жауабы: бүтін түбір x = 7. №3. Теңдеуді шешіңіз, жауапта түбірлердің қосындысын көрсетіңіз: 1). Ішкі модуль өрнектерінің нөлдерін табайық: x = 5; x = 1; x = - 2 2). Табылған мәндерді сандық сызықта белгілейміз және алынған аралықтарда әрбір модуль қандай белгімен ашылатынын анықтаймыз: x - 5 x - 5 x - 5 x - 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Теңдеудің x = 0 және 2 екі түбірі бар. Жауабы: түбірлердің қосындысы 2-ге тең. №4 . Теңдеуді шешіңіз: 1). Ішкі модуль өрнектерінің нөлдерін табайық: x = 1; x = 2; x = 3. 2). Алынған аралықтарда әрбір модуль кеңейтілетін белгіні анықтайық. 3).
Біріншісінің шешімдерін біріктірейік үш жүйе. Жауап: ; x = 5.
Жаттығулар: №24. Теңдеуді шеш:
№25. Теңдеуді шеш, жауапта түбірлердің қосындысын жаз: №26. Теңдеуді шешіңіз, жауапта кіші түбірді көрсетіңіз: №27. Теңдеуді шешіңіз, жауабыңызда үлкенірек түбірін беріңіз:

9-бөлім. Құрамында бірнеше модуль бар теңдеулер

Бірнеше модульден тұратын теңдеулер ішкі модуль өрнектерінде абсолютті мәндердің болуын болжайды. Бұл түрдегі теңдеулерді шешудің негізгі принципі «сыртқыдан» бастап модульдерді тізбектей ашу болып табылады. Шешім барысында No1, No3 бөлімдерде қарастырылған әдістер қолданылады.

Мысалдар: №1. Теңдеуді шеш:
Жауабы: x = 1; - он бір. №2. Теңдеуді шеш:
Жауабы: x = 0; 4; - 4. №3. Теңдеуді шешіңіз, жауапта түбірлердің көбейтіндісін көрсетіңіз:
Жауабы: Тамырлардың көбейтіндісі 8-ге тең. №4. Теңдеуді шеш:
Басымдық теңдеулерді белгілеңіз (1) Және (2) және дизайнға ыңғайлы болу үшін олардың әрқайсысының шешімін бөлек қарастырыңыз. Екі теңдеуде бірнеше модуль бар болғандықтан, жүйелер жиынына эквивалентті көшуді жүзеге асыру ыңғайлы. (1)

(2)


Жауап:
Жаттығулар: №36. Теңдеуді шешіңіз, жауапта түбірлердің қосындысын көрсетіңіз: 5 │3x-5│ \u003d 25 x №37. Теңдеуді шешіңіз, егер бірден көп түбір болса, жауапта түбірлердің қосындысын көрсетіңіз: │x + 2│ x - 3x - 10 = 1 №38. Теңдеуді шешіңіз: 3 │2x -4│ \u003d 9 │x│ №39. Теңдеуді шешіңіз, жауапта түбірлер санын көрсетіңіз: 2 │ sin x │ = √2 №40 . Теңдеуді шешіңіз, жауапта түбірлер санын көрсетіңіз:

3-бөлім. Логарифмдік теңдеулер.

Келесі теңдеулерді шешу алдында логарифмдердің қасиеттерін және қайталау қажет логарифмдік функция. Мысалдар: №1. Теңдеуді шешіңіз, жауапта түбірлердің көбейтіндісін көрсетіңіз: log 2 (x + 1) 2 + log 2 │x + 1 │ \u003d 6 O.D.Z. x+1≠0 x≠ - 1

1-жағдай: егер x ≥ - 1 болса, онда log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – x ≥ - 1 2 шартын қанағаттандырады: егер x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – x - 1 шартын қанағаттандырады
Жауабы: Тамырлардың көбейтіндісі 15-ке тең.
№2. Теңдеуді шешіңіз, жауапта түбірлердің қосындысын көрсетіңіз: lg
О.Д.З.

Жауабы: түбірлердің қосындысы 0,5.
№3. Теңдеуді шешіңіз: log 5
О.Д.З.

Жауабы: x = 9. №4. Теңдеуді шешіңіз: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Басқа негізге көшу формуласын қолданайық. │2 - журнал 5 x│+ 3 = │1 + журнал 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Ішкі модуль өрнектерінің нөлдерін табайық: x = 25; x \u003d Бұл сандар рұқсат етілген мәндердің ауданын үш интервалға бөледі, сондықтан теңдеу үш жүйенің жиынтығына тең.
Жауап:)